Dimensionality test
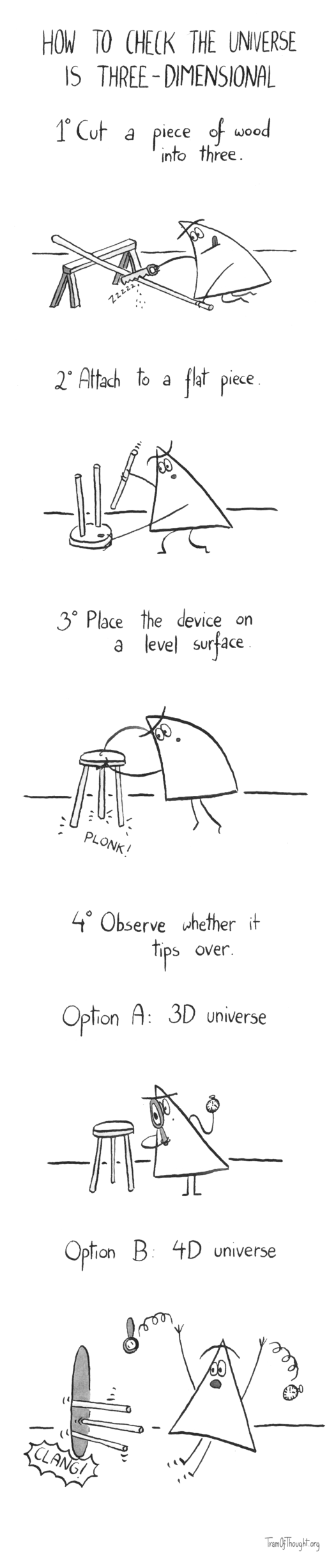
How to check the universe is three-dimensional
1° Cut a piece of wood into three
2° Attach to a flat piece
3° Place the device on a level surface
4° Observe whether it tips over
Option A: 3D universe
Option B: 4D universe
I’ve read in a book that for a stool to be stable in N spatial dimensions, it needs at least N legs of which no three share the same plane (I’m guessing we should be calling it a hyperplane, but I’m sure you intuitively know what I mean - a regular kitchen stool with three legs in one line would tip over).
Thus in our familiar 3D universe the stool needs three legs, each one stabilising the device against one dimension. In a 2D universe two legs would suffice - picture a flat stool drawn on a children’s image. In 1D only one leg is needed (but since there is only one dimension nothing will ever be able to tip over). In a 4D universe, an extra leg is needed which should reach out into the fourth dimension.
The last frame of this comic is attempting to show the 3-legged stool tipping over “into” the fourth dimension.
